Frozen Evolution. Or, that’s not the way it is, Mr. Darwin. A Farewell to Selfish Gene.

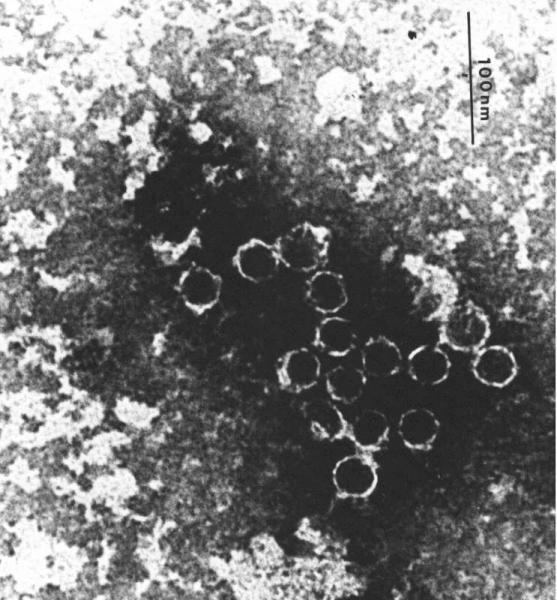
Box 23 Why to use established scientific methods

The answer is quite simple – because only by doing so is it possible to compare and therefore interconnect results obtained in different workplaces. Isolated results often don’t mean much; they achieve their true value only when related to other results from different scientists, often from studies dealing with entirely unrelated problems. For this reason, wherever at all possible, it’s best to use standard and preferably widely utilized methods. Scientists trained in former communist Czechoslovakia are often masters in the art of inventing new methods. Necessity indeed is the mother of invention – established methods were not available to them; they could not buy the appropriate standard chemicals nor tools, since funding for obtaining Western products was limited; and when funding happened to be sufficient, purchases from the outside had to be planned many years in advance, so that even if the long-desired instrument or chemical finally arrived, one had often forgotten, what he had needed it for. Under the communist regime the ability to improvise was the basic prerequisite for successful scientific practice, but today it is something of a two-edged sword. On one hand it allows the discovery of an oftentimes better, cheaper, faster or more effective method than that which is being standardly employed in a given field, but, on the other hand, results obtained through a nonstandard method are difficult to compare with results obtained in other workplaces (and of course also more difficult to publish in scientific journals). Newly developed methods often harbor unexpected obstacles. During my postdoctoral studies, for example, I tried to determine whether double-stranded RNA (dsRNA) present in Trichomonas cells floats freely in the cytoplasm or whether it is contained within virions. The standard method for isolating virions is separation of the cellular homogenate using the cesium chloride density-gradient ultracentrifugation. It is a time consuming method, the centrifugation itself spanning many hours; furthermore, cesium chloride is expensive, as is operating and maintaining the ultracentrifuge. I, however, discovered that I could obtain virions from the homogenate in less than an hour by precipitating them using the right concentration of cheap ammonium sulfate (3). In addition, I discovered that when I isolated nucleic acids in the presence of high concentrations of ammonium sulfate using acidic phenol instead of neutralized phenol (so I reached into the fridge and grabbed the wrong bottle, nobody’s perfect) all the DNA and single-stranded RNA disappeared – pure dsRNA remained in the resulting sample. The problem was that the electron microscopy showed these virions to be empty, devoid of any nucleic acids (fig. 16). I conceived daring hypotheses to explain this state of affairs, and tentatively allowed even for the possibility that the presence of virions might have nothing to do with the presence of dsRNA in Trichonomas cells. The reality was much more prosaic. During the nonstandard method of isolating virions by precipitation using ammonium sulfate, all the dsRNA escapes. Had I used the classical ultracentrifugation method, I would have saved myself a lot trouble.

Fig. 16 Viral particles observed by an electron microscope in the cellular homogenate of Trichomonas. When viral particles are precipitated by adding ammonium sulfate, all the nucleic acid molecules escape; therefore, the particles appear to be hollow. In reality, native particles contain double-stranded ribonucleic acid molecules. Photo by Jitka Štokrová.

Box 24 Types of variables from the perspective of statistics

In “normal, everyday life” we differentiate between quantitative variables (temperature, body height) and qualitative variables (nationality, gender). But in statistics it makes more sense to classify variables as continuous and discrete. Continuous variables, such as the above-mentioned temperature and body height, are free to take on any value (but usually only within a certain range of accepted values). Discrete variables encompass two types of data. The first type are ordinal variables, which can be ordered from lowest to highest, though the individual values don’t have to be equally spaced. One example of an ordinal variable is the level of education (primary, secondary, high); another is the degree of agreement with the statement in the questionnaire expressed on a given scale (strongly agree, mostly agree, not sure, mostly disagree, strongly disagree). The other type of discrete variables are categorical variables – these cannot be ordered by size. Among these are citizenship, the type of fertilizer or medicine used, etc. A special type of categorical variables are binary variables – these can take on only two values, like infected by Toxoplasma/uninfected by Toxoplasma, had a traffic accident/didn’t have a traffic accident, male/female. Based on the type of variable we must select the right type of statistical test. If, for example, we’re comparing the height of men and women, we’ll most likely use Student’s t-test; if it’s the education level of men and women, we’ll use some nonparametric test, like the Mann-Whitney U-test.

Box 25 Parametric and nonparametric tests

In practice, statistical tests are divided into parametric and nonparametric tests. Parametric tests, when used for the right type of data, are said to have more statistical power (that is, when they are used there exists a greater probability of a justified rejection of a null hypothesis) than corresponding nonparametric tests (see Box 21 Analysis of the power of a statistical test). This is understandable, since a parametric test uses a greater part of the information contained in the data: for example, it directly compares the body height of individuals in a group, whereas a nonparametric test uses but a small part of the information, most often the information about the order of the individuals according to their arrangement from tallest to shortest. In practice, the difference in the power of tests doesn’t tend to be great, usually under 10%. Parametric tests, however, are intended for data with a particular type of distribution, generally for continuous variables with a normal distribution. If our data has a different type of distribution – for example, if we’re dealing with ordinal data – a parametric test may yield a false result. In such a case it’s necessary to use a nonparametric test, or, where possible, a more powerful exact test, or at least a randomization test (see Box 83 Randomization tests).

If we’re comparing, for example, the average value of continuous data (like average height) between two groups (males and females), we’ll most likely use a parametric t-test; for multiple groups (Czechs, Germans, Chinese, English, Japanese), we’ll use the ANOVA (an analysis of variance). If we’re comparing paired continuous data (such as the body mass of the same mice before and after infection, see Box 67 What is the difference between the paired and unpaired t-tests, and why is the paired one better?), we’ll use a paired t-test. If we’re studying the effect of a certain factor taking on two or more levels (gender or ethnicity) and simultaneously the effect of another continuous variable (such as the age of the person) on a continuous variable (such as body mass), we’ll use an ANCOVA (an analysis of covariance). If we’re studying the effect of multiple independent factors, we’ll use the MANOVA instead of the ANOVA and the MANCOVA (multivariable analysis of variance and covariance) instead of the ANCOVA. If we’re simultaneously studying the effects of continuous and discrete variables (age, gender, size of residence) on binary variables (infected by Toxoplasma /uninfected by Toxoplasma), we’ll use a logistic regression, whereas for an ordinal variable we’ll use an ordinal logistic regression. If we’re studying the relationship of two continuous variables, we’ll use a correlation analysis, and if we also know or have decided beforehand which of the two variables is dependent (target) and which is explanatory, we’ll use a linear regression; if we’re studying the dependence of a continuous variable on multiple continuous variables, we’ll use a multidimensional linear regression. If we’re studying the relationship between two categorical variables, we’ll use contingency tables; if it’s between great numbers of categorical variables, we’ll use log-linear analysis. In all the above-mentioned cases we can also use the more universal GLM (General Linear Model) method, and, if needed, the even more universal GLZ (Generalized Linear Model method, often also donoted as GLM to make the orientation in the method more difficult for nonstatisticians). A nonparametric analogue of the common (unpaired) t-test is the Mann-Whitney U-test; an analogue of the paired t-test is the Wilcoxon test; an analogue of the simple ANOVA is the Kruskal-Wallis ANOVA; an approximate analogue of the two-way ANOVA is a Friedman test; and an analogue of correlation analysis is a Spearman’s rank correlation test, or a Kendall’s Tau test. Aside from hypotheses of the location (average, median value), we often test a hypothesis of the equality of the empirical and theoretical frequency distributions (most often using the Chi²-test); or we test a hypothesis of the equality of distribution of values in two or more sets (using the F-test); or a hypothesis of outlying values (using Grubbs’ or Dixon’s test).agreement with the statement: “I don’t have a strong sense of self-preservation: in situations, when others would probably be scared, at night alone in the woods or in a deserted house, I am not particularly afraid.” (P = 0.029).

We subsequently included the same questions, or at least some of them, in other questionnaire-based studies. We never again accomplished such strong associations with so many questions, yet even here the significant effect of toxoplasmosis on the subjects’ (blood donors, pregnant women) answers to some of these questions was apparent. Most often the test subjects mentioned that they have slower reflexes and that they believe that some people are able to impose their will on others using hypnosis or persuasion (17).

The statements which I set to our test subjects were relatively complex, each made up of multiple partial assertions. In the study which I carried out in the years 2007-2011, aside from the original ten complex statements, we also gave the students individual partial and specifying assertions. At the start of the 44-point questionnaire we presented the original ten statements, followed by 34 partial assertions, such as: “My instinctive (reflexive) behavior in situations of imminent danger is disproportionately slow or passive.” or “At night alone in a deserted house I’m not particularly afraid.” The students filled out the questionnaire on the computer, which recorded not only their answers, but also the time they needed to select each answer (this time on a 5-point scale). The final results of this more detailed study are not yet available.

I already mentioned that publishing a description of an unknown phenomenon studied using a nonstandard method doesn’t tend to be exactly easy. Nevertheless I succeeded that time, and, what’s more, right on the first try (17). Apparently my results were clear and convincing, and my argument bullet-proof enough, that neither the editor nor the reviewers were able to raise any substantial objections. But we cannot bar the possibility, that a certain role may have been played by the fact that the editor of this particular special journal number, and therefore also the person who selected the reviewers, was I.