Frozen Evolution. Or, that’s not the way it is, Mr. Darwin. A Farewell to Selfish Gene.

The model of r- and K-selection, also presented as the model of r- and K-strategy, was a popular concept of field ecology in their time (Pianka 1970).In nature, organisms with two fundamentally different life strategies can be encountered.One group of organisms prefers rapid reproduction.Its members are called r-strategists and the natural selection that they undergo is called r-selection.The second group tends to prefer the ability to compete with other organisms.The members of this group are called K-strategists and the relevant selection is called K-selection.

            The ecology of r-strategistsdiffers from that of K-strategists in a number of respects.Compared to K-strategists, they have shorter life cycles, greater maximum rate of reproduction, reproduce sooner, are usually smaller in size, frequently reproduce only once in their lifetime, and usually have a large number of progeny that, however, are not very viable and most of which do not even reach adulthood.The size of the populations of r-strategists tends to fluctuate in time and is mostly much smaller than would be permitted by the capacity of their environment, and thus within-species competition is very low.Death is usually caused by factors that do not differentiate amongst individuals according to genotype (random elimination, see below).r-Strategistsoccur particularly in a variable and unpredictable environment that is typical for the habitat in the early stages of succession.K-Strategistsbehave in the opposite way in all these respects.

            The names of the two ecological strategies were chosen on the basis of the traditional designation of the constants in the logistic equation(Fig. IV.2), i.e. the equation describing the growth of a population in an environment capable of sustaining only a limited number of individuals:

dN/dt = rN (K-N)/ K,

where N denotes the number of individuals in the population, r is the rate of growth and K is the capacity of the environment, corresponding to the maximum number of individuals that the given environment is capable of sustaining.The logistic equation is fundamentally only a modification of the polynomial

dN/dt = aN + bN²

where a = r, b = – r/K,

i.e. an equation that successfully describes the shape of the growth curve (rapid, almost exponential growth at the beginning and slowing down or even stopping after a high population density is achieved); however, in fact, it has very little in common with the actual mechanisms of regulation in populations limited by the availability of nutrition.

            The naming of the two types of natural selection according to the designation of the constants in the logistic equation is a very illustrative approach, but is rather unfortunate.To begin with, the logistic equation describes only a single, rather specific model of population growth, the specific case where the rate of reproduction is directly proportional to the size of the population and the death rate is directly proportional to the square of the size of the population – i.e., for example, population growth limited by a parasite transferred by direct contact.In addition, some authors noticed in the past that the existence of two types of natural selection does not follow from the logistic equation (Ginzburg 1992).We would expect that constant K would not play a role in a population of r-strategists and that the fitness of the organisms would be decided only by constant r, while the situation should be just the opposite in a population of K-strategists.However, in a population whose growth is described by the logistic equation, the fitness of an organism is affected to the same degree by constants r andK, so that there is only one strategy here, increasing r and/or K.Thus, although the concept of r- andK-strategies is one of the best known concepts in general ecology, the theoretical background of the relevant ecological phenomenon has so far been studied quite inadequately.

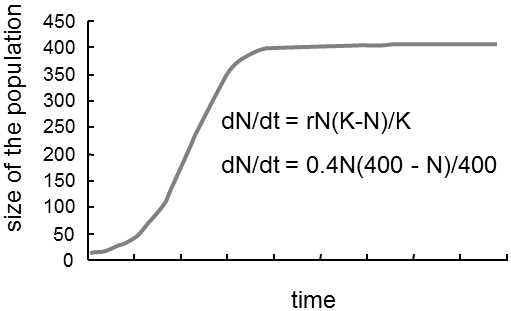
Fig. IV.2. Logistic equation. Population growth can be described by a logistic equation. It is usually stated that parameter r determines primarily the rate of growth of the population under conditions of excess of resources and parameter K, or, to be more exact, the value of r/K, determines the size of the population at the instant of maximum utilization of resources. In actual fact, the logistic equation is only an expression of the simplest function that permits phenomenological description of the normal behaviour of the population, i.e. initially gradually accelerating population growth that slows down after some time and finally completely stops