Frozen Evolution. Or, that’s not the way it is, Mr. Darwin. A Farewell to Selfish Gene.

In a great many cases, the fitness of the bearers of a trait depends only very indirectly on its frequency.An increase in the frequency of a particular trait increases the fitness (and subsequently also the frequency) of the bearers of another trait, an increase in the frequency of the bearers of a different trait increases the fitness of the bearers of this other trait and this subsequently reduces the fitness of the bearers of the first trait.In these complicated interconnected systems, the fate of new mutations is decided not so much by the Darwinist fitness of its bearers as by whether the presence of the given trait is an evolutionarily stable strategy (ESS) in the sense of game theory.Evolutionarily stable strategy is considered to constitute strategy that, as soon as it predominates in the population, will be more successful in every situation than any other minority strategy (Maynard Smith & Price 1973).Thus, if an allele that codes behaviour of an organism (strategy) that is evolutionarily stable predominates in the population, then no other allele that occurs in the population through migration or mutation can force it out of the population – see the definition of ESS above.

            A classical, albeit simplified example encompassing only two strategies in the basic variant, competition of only two strategies, on the basis of which evolutionarily stable strategy is studied, is the model of the dove and the hawk (Fig. IV.5).  Dove and hawk are names for two alternative strategies that can be adopted by two members of a single species when they clash, e.g., over a piece of food or some other scarce resource.The strategy of the dove consists in that the two individuals divide up the food.

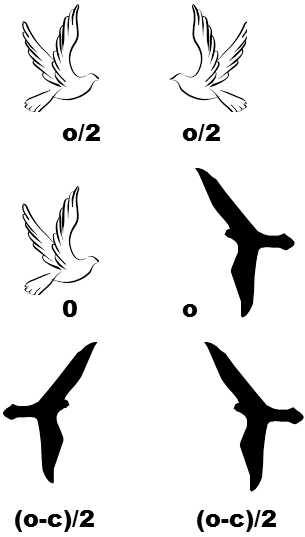
Fig. IV.5. The dove and the hawk. The pay-off matrix indicates the reward o obtained and the price c paid by a dove and a hawk in mutual conflicts.

In contrast, the strategy of the hawk is dependent on the fact that the two individuals fight for the food, the winner gains the whole piece and the loser remains only with its injuries.If a dove encounters a hawk, it retreats without a fight (and thus without injuries) and the hawk gains all the food for itself.Changes in the frequencies of the two strategies are dependent on how successful its bearers are in competition with the other members of the population, i.e. how much food (and how many injuries) they gain from mutual encounters.If a hawk comes into a population of doves, it is initially very well off as it wins all the encounters without a fight and obtains all the food.The frequency of hawks thus increases in the population.Similarly, if a dove enters a population of hawks, it is initially at an advantage in competition with the other members of the population.It always gives up in advance in any fight for food (however, it will certainly occasionally find some food when a hawk is not close-by); however, in conflicts with other hawks, an average hawk will end up with injuries in half the cases.It is apparent that, in the end, a stable ratio of doves and hawks will be established in the population, at which the average fitness of doves and hawks will be identical.The specific value of this ratio is determined by the by the values of the pay-off matrix.The following scheme gives an example of such a matrix.If two doves meet over a piece of food, each obtains an average gain of o/2 (where o is the average value of one piece of food expressed as input of biological fitness for the individual that consumes it).If two hawks meet, each of them gains, on an average, (o – c)/2 (where c is the average loss connected with injuries suffered in conflict of two hawks over prey, again expressed as the reduction in biological fitness of the injured individual).If a hawk encounters a dove, the hawk obtains gain o and the dove does not obtain any gain (but also suffers no loss).The average gain of a hawk in all conflicts (with doves and hawks) depends on the presence of the two strategies in the population and is equal to

           Z _j = p(o-c)/2+(1-p)o,                                                                                                        (1)                            

where p is the frequency of hawks in the population.The similar average gain of a dove is

           Z_h = p.0+(1-p) o/2.                                                                                                              (2)

The population moves towards an equilibrium state, at which the average gain of the representatives of the two strategies is equal and where it holds that Z_h = Z_d.Substitution into equations (1) and (2) yields

p(o-c)/2+(1-p)o = 0+(1-p)o/2                                                                                                         (3)

Following simple modification, this equation yields the frequency of hawks in the equilibrium population

p=o/c                                                                                                                               (4)

Neither the strategy of the dove nor the strategy of the hawk is evolutionarily stable.On the other hand, the strategy “behave like a hawk with frequency o/c and like a dove with frequency of (1 – o/c)” is evolutionarily stable; if an allele that determines this behaviour predominates in the population, no other allele will be capable of successfully penetrating into the population.The basic model of the dove and hawk can be variously further developed (see also XVI.9).For example, interesting situations occur if we admit the existence of other strategies, such as the strategy “act like a hawk at the beginning of an encounter but, as soon as you encounter resistance, run away” or the strategy “act like a dove initially but, as soon as you are attacked, begin to fight like a hawk”.In some models, we find that a particular strategy acts as evolutionarily stable only until two different alternative strategies are present in the population; in other cases, the frequency of a certain strategy begins to increase but is completely forced out by some other strategy after a certain period of time (a strategy that had no chance of spreading under the initial conditions).

            Most people erroneously understand strategy to refer to the particular behaviour of an animal or human being.However, the theory of evolutionarily stable strategies is certainly not related only to the evolution of individual patterns of behaviour.From the standpoint of the theory and the mathematical apparatus employed, it makes no difference whether we study the competition of the alleles that code a certain pattern of behaviour of their bearers, or alleles that code, e.g., the synthesis of a certain pigment or enzyme.Competition for an evolutionarily stable strategy is applied almost universally for sexually reproducing organisms.In these organisms, the fitness of the bearers of certain alleles is rarely determined by an unvarying selection coefficient, but is rather usually dependent on the frequency with which it encounters other alleles of the same or some other gene in the future embryos, i.e. on which alleles will probably be borne by both parents of the future progeny.