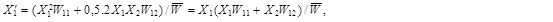IV.6.1 The models of population genetics make it possible to calculate the progress of changes in the frequency of a dominant, recessive or superdominant allele.

Study of the changes in the frequency of alleles in a certain gene can be based on the following model:We have a population of randomly cross-breeding diploidal organisms.The population is sufficiently large so that no random processes are important and thus there are no random fluctuations in the size of the population and frequencies of the individual alleles, reproduction of organisms and selection processes are synchronous and the individual generations are discrete, i.e. do not overlap.The studied gene has only two alleles, A1andA2, whose frequencies are X1a X2, where X1 = 1 –X2.The fitnesses of the three possible genotypes A1A1, A1A2 andA2A2  are in the order W11, W12andW22 and their frequencies prior to the action of selection are  and, i.e. they are subject to the Hardy-Weinberger equilibrium.The frequency X1of the following generation is given by the equation:

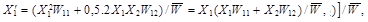(1)

  where    is the average fitness of the population

 

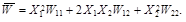                                                                                               (2)

 

A change in frequency X1in a generation is given by the equation

 

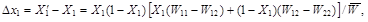                                                 (3)

 

which, following substitution from equation (2), yields

 

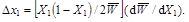                                                                                                          (4)

 

As  depends on the relative and not the absolute values of W11, W12, W22, these quantities can be set equal in the series 1, 1 – s1, 1 – s2.Symbols s1 and s2 denote selection coefficients expressing the degree of selection pressure against the individual genotypes.

            It holds for the semidominant allele A1, whereW11 = 1, W12 = 1 – s/2, W22 = 1 – s (the heterozygote exhibits the relevant trait to a smaller degree, in the analyzed case to half the degree of the homozygote A2A2), that

 

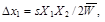                                                                                                                   (5)

 

for allele A1 with complete dominance, where W11 = W12 = 1, W22 = 1 – s (the heterozygote has the same phenotype and thus the same fitness as the homozygote A1A1) it holds that

 

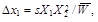                                                                                                                     (6)

 

for the recessive allele A1, where W11 = 1, W12 = W22 = 1 – s (the heterozygote has the same phenotype as the homozygote A1A1), it holds that

 

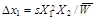                                                                                                                     (7)

 

and, for the case of superdominance, where W11 = 1 – s1, W12 = 1, W22 = 1 – s2 (the hereozygote has greater fitness), it holds that

 

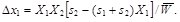                                                                                                (8)

 

Equations (5) – (8) are nonlinear, so that it is easier to solve them numerically.In equations (5) – (7), the frequency of allele A1gradually increases to complete suppression of allele A2.For the cases of dominance and semidominance, the increase is relatively rapid; in the case of recessivity, selection occurs very slowly and accelerates substantially only after an increase in the frequency above a certainvalue (Fig.IV.6).In case of superdominance, is positive while

 

 

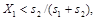
If X1 increases above this value, then x1is negative.This thus means that there exists an equilibrium frequency of allele A1(R), for which it holds that

 

R = s2  /( s1  +  s2 ),                                                                                                       (9)

 

i.e., a frequency that the population sooner or later attains and to which it returns after any fluctuations.

            If the selection coefficient is low, then fitness  is approximately equal to 1 and  is very small, so that equation (3) can be replaced by the equation

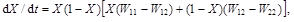                                       (10)

where X = X1and t is time expressed in the number of generation periods.It holds for the semidominant allele that

 

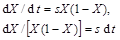                                                                                                              (11)

 

and, after integration

 

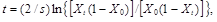                                                                                       (12)

 

where X0 and Xt  are the frequencies of allele A1at times 0 and t.For the dominant allele we similarly obtain the equation

 

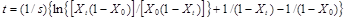                                                     (13)

 

and, for the recessive allele,

 

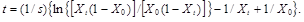                                                     (14)

                                                                    

 

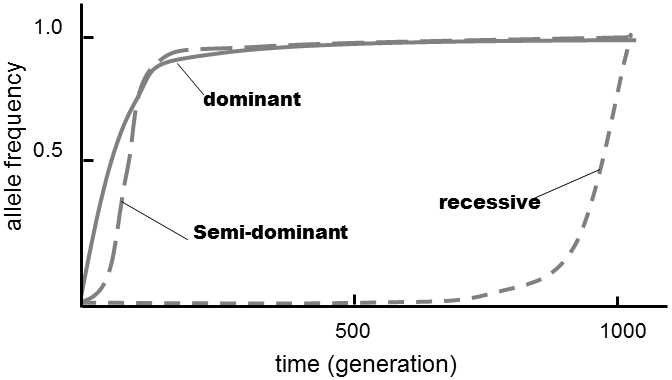
Fig. IV.6. Selection in favour of advantageous dominant, semi-dominant and recessive alleles. The action of selection leads to the fastest increase in the content of dominant alleles and the slowest in the content of recessive alleles. However, semi-dominant alleles become fixed soonest.

Equations (12), (13) and (14) permit determination of the number of generations necessary to change the frequency of allele A1from the initial frequency X0 to the final frequency Xt.

Was this information useful for you?
The classical Darwinian theory of evolution can explain the evolution of adaptive traits only in asexual organisms. The frozen plasticity theory is much more general: It can also explain the origin and evolution of adaptive traits in both asexual and sexual organisms Read more
Draft translation from: Evoluční biologie, 2. vydání (Evolutionary biology, 2nd edition), J. Flegr, Academia Prague 2009. The translation was not done by biologist, therefore any suggestion concerning proper scientific terminology and language usage are highly welcomed. You can send your comments to flegratcesnet [dot] cz. Thank you.