Frozen Evolution. Or, that’s not the way it is, Mr. Darwin. A Farewell to Selfish Gene.

So far, we have considered only the action of genetic drift on neutral traits.However, from the standpoint of evolution, the behavior of selectionally important traits is far more important, i.e. traits whose frequency in the population changes through the action of natural selection.

            The probability and the rate of fixation of selectionally important mutations through genetic drift depends on the effectiveness of genetic drift in the given population and the selection coefficient for the given mutation (Fig. V.10).M. Kimura studied the dependence of fixation of mutations on these factors.He showed that the probability of fixation of a mutation (o) can be calculated from the equation:

p = (1- e^-4sqN_e )/(1 - e^-4sN_e   ),                                                  (6)       

where N_eis the effective size of the population, s is the selection coefficient of the relevant mutation and q is its initial frequency in the population.As it holds for small x approximately that  e^-x = 1-x ,this is reduced for very small s (neutral or almost neutral mutation) to the familiar relationship p = q, i.e. the probability of fixation of a neutral mutation is equal to its initial frequency in the population.

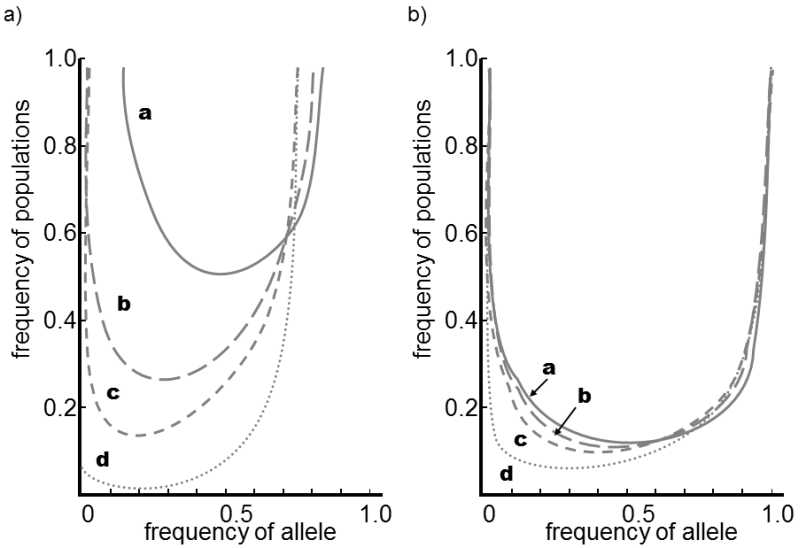
Fig. V.10. Mutual interplay of selection and genetic drift. In a population of heterozygotes divided at time t₀ into a large number of separate populations with size N, over a sufficient number of generations the action of genetic drift creates a state where the numbers of individual small populations with certain frequencies of the studied alleles will have U-shaped distribution (see also Fig. V.3). If the bearers of one of the alleles are favored by selection compared to bearers of the second allele, the distribution will have highly asymmetrical shape as the population with a greater frequency of the more advantageous allele will predominate in the set. The greater the selection advantage of one of the alleles, the closer will be the shape of the distribution to curve d in graph (a). However, if a substantially smaller population (b) is involved, the effect of genetic drift will predominate over the effect of selection and the shapes of the distribution curves will depend very little on the selection coefficient. In the given case, the frequencies of the two alleles were identical at time t₀; in case (a), the population size n was four times greater than in case (b) and the selection coefficients for the less advantageous allele were equal to 0, 1/2N, 1/N and 2/N for curves a, b, c and d, respectively.

           If this is a new mutation in a population of diploid organisms (q = 1/2N), the equation assumes the form

p = (1 - e^2sN_e/N  )/( 1 - e^-4sN_e )                                                                  (7)

The familiar equation p = 1/2N is obtained for neutral mutations.

            For cases where the effective size of the population is equal to the size of the real population, the equation would have the form:

p = (1-e^-2s  )(1-e^-4Ns  )                                                                               (8)

If the absolute value of the selection coefficient is small, it will hold approximately that:

     p =  2s/(1-e^-4Ns    )                                                                                   (9)

For small positive s and large N, this equation is reduced to

p= 2s.                                                                                                              (10)

This means that, in a large population, the probability of fixation of a weakly positive mutation is approximately equal to twice its selection coefficient.Specifically, the probability of fixation of a mutation with selection coefficient s = 0.01 is approximately 2%.

            The probability of fixation of various types of mutations can best be illustrated on specific cases.In a population of diploid organisms for which it holds that N = N_e = 1000, a neutral mutation will become fixed with a probability of 0.05%, a weakly positive mutation (s = 0.01) with a probability of 2% and a weakly negative mutation (s = 0.001) with a probability of 0.004%.

            The average time of fixation of a mutation was calculated by Kimura and Ohta for neutral mutations in a population of diploid organisms as t = 4N_e generation periods and, for selectionally significant mutations as t = 2/s ln 2N_e generation periods.

            For diploid organisms with a generation period of 2 years and effective population size of N_e = 10⁶,fixation of a neutral mutation takes approximately 8 million years but fixation of a mutation with a selection coefficient of 0.01 takes only 5800 years.It is interesting that fixation of a negative mutation with a selection coefficient of -0.01 also requires an average of 5800 years.It is obvious that a negative mutation will become fixed in the population with far lower probability and thus far less often; however, those that do become fixed are fixed very rapidly.

            The frequency of fixation of mutations k is equal to the product of the frequency of the formation of the mutations u and the probability of their fixation p.For neutral mutations, we derived that k = 2Nu/2N = u.For selectionally advantageous mutations, the following equation is obtained in a similar manner

k = 4Nsu.

It is important to emphasize here that the rate of fixation of selectionally significant mutations, i.e. fixation of mutations through natural selection, depends, not only on their selectional advantageousness, but also on the size of the population in which the natural selection acts.In large populations, the action of natural selection is significant, while natural selection has practically no importance in small populations.