Frozen Evolution. Or, that’s not the way it is, Mr. Darwin. A Farewell to Selfish Gene.

The extreme intricacy, complexity of living organisms is one of their most ostensible characteristics that is immediately obvious compared to any type of nonliving system. However, it is not at all clear how this property should be best defined and it is certainly not clear to which degree it is actually related to the process of biological evolution.

Sometimes, the complexity of a system is understood and defined on the basis of the number of its elements or, at other times, on the basis on the number of various interactions amongst its elements (Fig. I.1). Relatively exact verbal definitions of the complexity of systems assume that this is directly proportional to the length of the shortest possible description of the relevant system, or the length of the algorithm that can be used to generate the particular system or its model. However, in this case, substantial complications arise from determination of the complexity of the fractal shapes as their frequently enormous complexity can often be formed using very simple algorithms (Fig. I.1). McShea (1996), for example, gives a summary overview of this aspect.

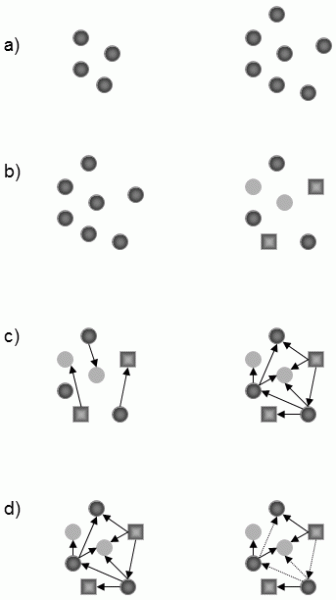
Fig. I.1 The complexity of systems. The criterion of complexity can be the number of elements in the system (a), the variety of the elements of the system (b), the number of bonds between the elements (c) or the variety of the bonds between the elements of the system (d). However, real systems usually differ in several aspects simultaneously. Thus, when comparing their complexity, it is necessary to state which criteria we prefer in the given case.

It is quite apparent that biological evolution does not always lead from simpler systems to more complicated systems; in fact, it frequently leads in the opposite direction, for example to the radical simplification of certain organ systems in some parasitic organisms. The generally held idea that the complexity of living organisms increases during evolution is probably

Fig. I.2 Fractals. The graphical depiction of the Mandelbrot set (a) is a well-known example of a fractal. This set includes elements that belong to the plane of complex numbers (in the figure, the abscissa corresponds to the real part and the ordinate corresponds to the imaginary part of a particular complex number c) that, even after infinitely repeated substitution into the (recurrent) equation z_n+1 = z_n² + c (where z₀=0), does not exceed a value of 2. Some points in the plane exceed a value of 2 in the very first substitution into the equation, while this occurs for others only when the given procedure, i.e. addition to its square and substitution of the result into the right-hand side of the equation, is repeated many times. The number of these iterations required to exclude that a particular point belongs to the Mandelbrot set is depicted by the degree of grey in the figure. (A much nicer picture is created when the numbers of iterations are depicted in various colours.) The areas in the plane of complex numbers for which 170 iteration steps still did not lead to exceeding a value of 2 and that could thus belong in the Mandelbrot set are depicted in black in the figure. This simple algorithm leads to an extremely complicated shape whose individual parts can be constantly zoomed in and further and further details can be found in them  (b, c, d, e, f). The figures were created using the excellent program XAOS, which was available free in 2008 on the web site http://wmi.math.u-szeged.hu/xaos/doku.php. Several i-Pad applications, e.g. FastFractal, are also available at App Store.

based on our natural experience. Organisms that evolved in the later stags of evolution, such as chimpanzees, mostly seem more complicated to us than evolutionarily older organisms, such as the bacteria Escherichia coli (see also XXVI.6). However, natural experience may be misleading. Because of the increasing overall number of species, it is not possible to simply compare a representative of evolutionarily older species with a representative of evolutionarily younger species – amongst other things, it would be necessary to compare the complexity of average representatives of the two types of organisms. The complexity of a species apparently does not increase within a single species (by microevolutionary mechanisms). Detailed exact analysis of macroevolutionary trends has been performed for only a very few taxons (comparison of complexity within pairs of parent and daughter species) and the results obtained are rather ambiguous (McShea 1994; McShea 1996). In addition, it seems that, where there is evidence indicating the existence of a trend towards increasing complexity, this will most probably be a passive trend, i.e. a trend caused simply by the fact that, at the beginning of evolution, the complexity of organisms was so small that any change could lead only to an increase (McShea 1996; Gould 1994). This phenomenon is usually denoted as the wall effect (Fig. I.3).

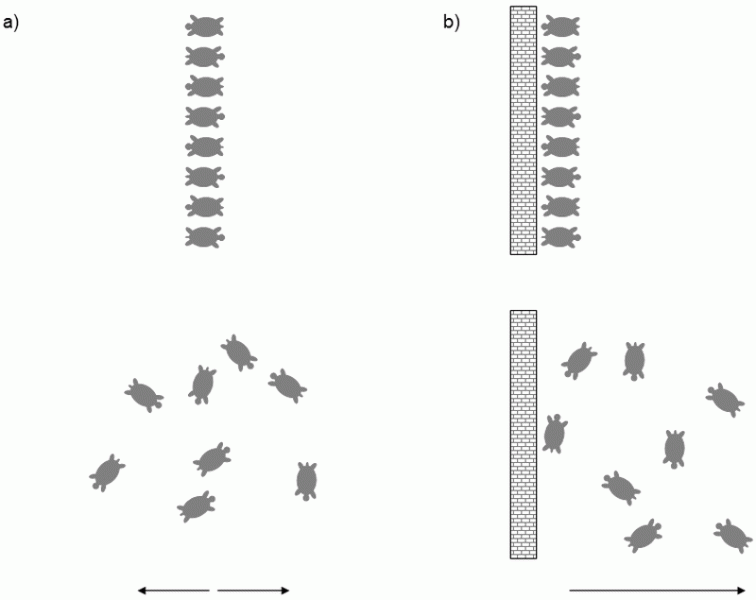
Fig. I.3 The wall effect. If individuals can move in an arbitrary direction, the population as a whole more or less remains in one place (a). However, if an impermeable barrier prevents their movement in a particular direction, the population gradually moves away from it (b). In evolution, a barrier can be created, e.g., by the minimum complexity necessary for the functioning of a living system.