Frozen Evolution. Or, that’s not the way it is, Mr. Darwin. A Farewell to Selfish Gene.

The quality of the results obtained can be evaluated on the basis of statistical tests and the reliability of the individual results included in the analysis by calculation of the indices of consistency, retention orhomoplasy.In the former case, for example, Student’s t-test statistics are calculated from the difference in the anticipated numbers of evolutionary changes in the two compared trees (D), from the variability in these differences for the individual traits (V_D) and from the number of traits (n) included in the analysis:

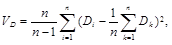
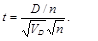
It is subsequently determined from the t-test tables for (n – 1) degrees of freedom whether there is a statistically significant difference between the compared tress in the minimum number of required evolutionary changes and thus in the ability to explain the distribution of traits between the compared phylogenetic trees.

Assessment of the quality of trees and of data generally takes into account the ratio of the numbers of homologies and homoplasies.The indices of consistency, retention and homoplasy are calculated for this purpose.The simplest of these is the consistency index (CI), which gives the ratio of the minimum number of evolutionary changes in the given trait (m), i.e. a number by one unit smaller than the number of various forms of the given trait in our dataset, to the number of evolutionary changes in the given trait assuming validity of the particular tree (s).For one trait, the consistency index is denoted as ci and is calculated as

      ci = m/s

For the whole tree formed on the basis of n traits, it is denoted as CI and is calculated as

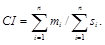
If the value of this index for a certain trait is low compared with the values for the other traits, the trait is not very suitable for phylogenetic analysis, as this is probably a trait that is too variable.As soon as a trait is repeatedly formed and disappears during phylogenesis, it is not possible to differentiate in which of the compared species it corresponds to homologies and in which homoplasies.The larger the CI value obtained for the particular tree, the smaller the fraction of homoplasy that is probably contained by our data.However, the values of the consistency indices depend not only on the quality of the data but also on the topology of a particular tree.Thus, it is preferable in comparing independently formed trees to use the retention index (RI) instead of the consistency index; the retention index is not characterized by this kind of dependence and, in addition, it varies within a closed interval á0-1ñ.The retention index for one trait (ri) is calculated as

ri = ( g -s)/(g-m)

and, for the whole tree

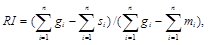
where g is the necessary number of evolutionary changes in the i^thtrait for the tree to have star-like topology, where the ancestor from which all the studied species immediately branched off would carry the commonest form of the particular trait.In some cases, the rescaled consistency index (RCI) is used as a measure of the data quality.This index is calculated by multiplying the consistency index by the retention index.

The homoplasy index (HI) can be determined from the retention index.

HI = 1 - RI.

Even a tree with a high retention index can, of course, be erroneous.It is always useful to test the correctness of the obtained evolutionary scheme on the basis of other traits that were not originally used in construction of the tree or to try to verify the hypothesis on the distribution of traits into homologies and homoplasies using other independent methods.